Algorithm - Kalman Filter Part 2
11 Oct 2022 - nguyenthanhminh1. Nhắc lại về Kalman Filter
Mình sẽ tóm tắt Kalman Filter dưới dạng các ký hiệu toán học và không giải thích như phần 1 nữa, các bạn nếu chưa hiểu rõ có thể quay lại phần 1.
Kalman Filter gồm các thành phần như sau:
$\mathbf{x}\in \mathbb{R}^{n}$ là trạng thái của object có kèm theo yếu tố thời gian.
$ \mathbf{F} \in \mathbb{R}^{n*n}$ là mô hình chuyển đổi trạng thái (The state-transition model).
\[\mathbf{x}^{t+1} = \mathbf{F}*\mathbf{x}^{t} + \mathbf{w}^{t} \hspace{1cm} (\text{1-1})\]$\mathbf{w} \thicksim \mathcal{N}(0, \mathbf{Q}) \in \mathbb{R}^{n}$ là nhiễu của dự đoán.
Ta xem $\mathbf{x} \thicksim \mathcal{N}(\overline{x}, \Sigma_{x})$. Gọi $\Sigma_{x}$ là ma trận covariance của x kèm yếu tố thời gian, và kỳ vọng là $\overline{x}$.
$\mathbf{y}\in \mathbb{R}^{m}$ là quan sát của object kèm theo yếu tố thời gian.
$ \mathbf{H} \in \mathbb{R}^{m*n}$ là mô hình quan sát (The observation model).
\[\mathbf{y}^{t} = \mathbf{H}*\mathbf{x}^{t} + \mathbf{v}^{t} \hspace{1cm} (\text{1-2})\]$\mathbf{v} \thicksim \mathcal{N}(0, \mathbf{R}) \in \mathbb{R}^{m}$ là nhiễu của quan sát.
Ta xem $\mathbf{y} \thicksim \mathcal{N}(\overline{y}, \Sigma_{y})$. Gọi $\Sigma_{y}$ là ma trận covariance của x kèm yếu tố thời gian, và kỳ vọng là $\overline{y}$.
Diễn giải dưới đây được dẫn từ Thetalog, mình khuyên các bạn cũng nên đọc Thetalog để có thể hiểu rõ hơn về Kalman Filter.
Ta có giả định:
\[\mathbf{y}^{t} = \mathbf{H}*\mathbf{x}^{t} + \mathbf{v}^{t}\]Nhưng việc biết $\mathbf{y}^{t}$ sẽ giúp gì cho lần cập nhật tiếp theo? Xét biểu thức:
\[p(x^{t}|y^{t}) = \frac{p(y^{t},x^{t})}{p(y^{t})} \hspace{1cm} (\text{1-3})\]Trong đó:
$p(x^{t}|y^{t})$ là hàm phân bố xác suất của $\mathbf{x}^{t}$ khi biết $\mathbf{y}^{t}$
$p(y^{t},x^{t})$
là hàm phân bố xác suất đồng thời của
$\mathbf{y}^{t}$
và
$\mathbf{x}^{t}$
$p(y^{t})$ và $p(x^{t})$ lần lượt là hàm phân bố xác suất của $\mathbf{y}^{t}$ và $\mathbf{x}^{t}$
Lúc này việc có thông tin về $\mathbf{y}^{t}$ sẽ giúp chúng ta cập nhật lại hàm phân bố xác suất cho $\mathbf{x}^{t}$ thông qua $p(x^{t}|y^{t}).$ Từ đó những quan sát tiếp theo sẽ mang độ chính xác cao hơn.
2. Hệ số Kalman
\[\mathbf{K}^{t+1} = \Sigma_{x}^{t+1}*\mathbf{H}^{\mathbf{T}} (\mathbf{R} + \mathbf{H}*\Sigma_{x}^{t+1}*\mathbf{H}^{\mathbf{T}})^{-1} \hspace{1cm} \text{(2-1)}\]Các blog hiện nay đa số đều bỏ qua đi phần chứng minh này, nhưng mình sẽ chứng minh từng bước cho bạn thấy từ đâu mà hệ số $Kalman$ xuất hiện.
Lưu ý từ đây sẽ nồng nặc mùi toán học, hãy đọc chậm rãi và cẩn thận nhé. Chúng ta sẽ chứng minh các bài toán nhỏ để ra được hệ số Kalman hoàn thiện nhé.
2.1 Schur Complement of matrix
Cụ thể “Schur Complement of matrix” biểu diễn ma trận $\mathbf{M}^{-1}$ dựa trên 4 khối ma trận nằm trong ma trận $\mathbf{M}$ vuông. Để hiểu được phần này, bạn cần kiến thức về Block matrix.
Xét ma trận $\mathbf{M}$ gồm $2 \times 2$ các khối $matrix$:
\[\mathbf{M} = \begin{bmatrix} \mathbf{A} & \mathbf{B} \\ \mathbf{B}^\mathsf{T} & \mathbf{D} \end{bmatrix} \hspace{1cm} (\text{2.1-1})\]Với $\mathbf{A} \in \mathbb{R}^{p \times p}$, $\mathbf{B} \in \mathbb{R}^{p \times q}$ và $\mathbf{D} \in \mathbb{R}^{q \times q}$. Có thể suy ra kích thước của $\mathbf{M}\in \mathbb{R}^{(p+q) \times (p+q)}$
Ở đây minh sẽ chứng minh cho trường hợp đặt biệt, còn tổng quát bạn hãy thay $\mathbf{B}^{T}$ thành $\mathbf{C}$ là được nhé, cũng có thể xem như là bài tập dành cho bạn để quen với ma trận hơn.
Để giải bài toán này cũng cực kỳ đơn giản, hẳn là bạn đã từng giải qua hệ phương trình bằng ma trận rồi phải không.
\[\mathbf{M} \times \mathbf{a} = \mathbf{b} \Rightarrow \mathbf{a} = \mathbf{M}^{-1} \times \mathbf{b} \hspace{1cm} (\text{2.1-2})\]Note: ở đây $x$, $y$ là các $vector \in \mathbb{R}^{(p+q)}$, và mỗi khi $matrix^{-1}$ ta giả sử $matrix$ khả nghịch
Cho:
\[\mathbf{a} = \begin{bmatrix} \mathbf{x} \\ \mathbf{y} \end{bmatrix}; \space \mathbf{b} = \begin{bmatrix} \mathbf{u} \\ \mathbf{v} \end{bmatrix} ;\space a, u \in \mathbb{R}^{p} \space và \space b, v \in \mathbb{R}^{q}\]Từ $(\text{2.1-1})$ và $(\text{2.1-2})$ ta có:
\[\mathbf{M} \times \mathbf{x} = \mathbf{y} \Leftrightarrow \begin{bmatrix} \mathbf{A} & \mathbf{B} \\ \mathbf{B}^\mathsf{T} & \mathbf{D} \end{bmatrix} \times \begin{bmatrix} \mathbf{x} \\ \mathbf{y} \end{bmatrix} = \begin{bmatrix} \mathbf{u} \\ \mathbf{v} \end{bmatrix} \hspace{1cm} (\text{2.1-3})\] \[\Rightarrow \begin{bmatrix} \mathbf{A} \mathbf{x} + \mathbf{B}y \\ \mathbf{B}^\mathsf{T}\mathbf{x} + \mathbf{D}\mathbf{y} \end{bmatrix}= \begin{bmatrix} \mathbf{u} \\ \mathbf{v} \end{bmatrix} \hspace{1cm} ((\text{2.1-4})\]Từ $((\text{2.1-4})$ ta đi sẽ tìm $\mathbf{x}$ và $\mathbf{y}$:
Ở dòng thứ hai của $((\text{2.1-4})$:
\[\mathbf{y} = \mathbf{D}^{-1}(\mathbf{v}-\mathbf{B}^\mathsf{T}\mathbf{x}) \hspace{1cm} (\text{2.1-5})\]Thế $((\text{2.1-5})$ vào dòng thứ nhất của $((\text{2.1-4})$:
\[\mathbf{A} \mathbf{x} + \mathbf{B}\mathbf{D}^{-1}(\mathbf{v}-\mathbf{B}^\mathsf{T}\mathbf{x}) = \mathbf{u} \Leftrightarrow (\mathbf{A} - \mathbf{B}\mathbf{D}^{-1}\mathbf{B}^\mathsf{T})\mathbf{x} = \mathbf{u} - \mathbf{B}\mathbf{D}^{-1}\mathbf{v} \hspace{1cm} (\text{2.1-6})\]Kết hợp giữa $((\text{2.1-5})$ và $(\text{2.1-6})$ ta có được:
\[\mathbf{x} = (\mathbf{A} - \mathbf{B}\mathbf{D}^{-1}\mathbf{B}^\mathsf{T})^{-1}\mathbf{u} - (\mathbf{A} - \mathbf{B}\mathbf{D}^{-1}\mathbf{B}^\mathsf{T})^{-1}\mathbf{B}\mathbf{D}^{-1}\mathbf{v} \hspace{1cm} (\text{2.1-7})\] \[\mathbf{y=-D^{-1}B^\mathsf{T}(A-BD^{-1}B^\mathsf{T})^{-1}u + (D^{-1} + D^{-1}B^\mathsf{T}(A-BD^{-1}B^\mathsf{T})^{-1}BD^{-1})v} \hspace{1cm} (\text{2.1-8})\]Ta đặt $\mathbf{L = (A-BD^{-1}B^\mathsf{T})^{-1}}$ để biểu thức đơn giản hơn, ta viết lại biểu thức $(\text{2.1-7})$ và $(\text{2.1-8})$.
\[\mathbf{x = Lu - LBD^{-1}v}\hspace{1cm} (\text{2.1-9})\] \[\mathbf{y=-D^{-1}B^{\mathsf{T}}Lu + (D^{-1} + D^{-1}B^\mathsf{T}LBD^{-1})v} \hspace{1cm} (\text{2.1-10})\]Dễ dàng thấy được:
\[\begin{bmatrix} \mathbf{x} \\ \mathbf{y} \end{bmatrix} = \begin{bmatrix} \mathbf{L} & \mathbf{-LBD^{-1}} \\ \mathbf{-D^{-1}B^{\mathsf{T}}L} & \mathbf{D^{-1} + D^{-1}B^\mathsf{T}LBD^{-1}} \end{bmatrix} \begin{bmatrix} \mathbf{u} \\ \mathbf{v} \end{bmatrix} \hspace{1cm} (\text{2.1-11})\]Kết hợp giữa $(\text{2.1-2})$ và $(\text{2.1-11})$, ta có được:
\[\mathbf{M} = \begin{bmatrix} \mathbf{A} & \mathbf{B} \\ \mathbf{B}^\mathsf{T} & \mathbf{D} \end{bmatrix}^{-1} = \begin{bmatrix} \mathbf{L} & \mathbf{-LBD^{-1}} \\ \mathbf{-D^{-1}B^{\mathsf{T}}L} & \mathbf{D^{-1} + D^{-1}B^\mathsf{T}LBD^{-1}} \end{bmatrix} \space với\space \mathbf{L = (A-BD^{-1}B^\mathsf{T})^{-1}} \hspace{1cm} (\text{2.1-12})\]Thế là ta đã xong với việc biểu diễn một ma trận nghịch đảo của ma trận vuông $\mathbf{M}$ dựa vào 4 khối ma trận con bên trong nó. Bạn có thấy ma trận này quen không, đúng rồi đấy nó chính là ma trận covariance $\Sigma_z$.
Với:
\[\mathbf{z} = \begin{bmatrix} \mathbf{x} \\ \mathbf{y} \end{bmatrix};\space \mathbf{x}\in \mathbb{R}^{p}, \space \mathbf{y}\in \mathbb{R}^{q}\]Và:
\[\mathbf{z} \thicksim \mathcal{N}(\mu_z,\Sigma_z) \Leftrightarrow \mathbf{z} \thicksim \mathcal{N}( \begin{bmatrix} \mu_x \\ \mu_y \end{bmatrix}, \begin{bmatrix} \Sigma_{xx} & \Sigma_{xy} \\ \Sigma_{yx} & \Sigma_{yy} \end{bmatrix})\]Vì đây cũng là một bài toán không quá khó và cũng khá dễ hiểu nếu bạn vững các kiến thức về ma trận, độc giả có thể đọc thêm về Multivariate Gaussian Distribution để hiểu rõ về ma trận covariance này, vì về sau ta sẽ dùng nó nhiều đấy.
2.2 Woodbury Matrix Identity
Woodbury Matrix Identity - Đồng nhất thức ma trận Woodbury, đồng nhất thức giúp tính toán biểu thức $\mathbf{(A+UCV)^{-1}}$ nhanh chóng hơn khi đã biết $\mathbf{A^{-1}}$.
Kích thước của các ma trận: $\mathbf{A} \in \mathbb{R}^{n \times n}$, $\mathbf{U, V} \in \mathbb{R}^{n \times k}$ và $\mathbf{C} \in \mathbb{R}^{k \times k}$ và công thức của nó là:
\[\mathbf{(A+UCV)^{-1} = A^{-1} - A^{-1}U(C^{-1}+VA^{-1}U)^{-1}VA^{-1}} \hspace{1cm} (\text{2.2-1})\]😱😱😱 Cái gì thế này, chẳng phải phía trên đã bảo sẽ giúp tính toán nhanh hơn cơ mà, sao mà lại dài đến như thế này!!!
Vậy chúng ta hãy lần lượt phân tích chi phí tính toán của biểu thức $\mathbf{(A+UCV)^{-1}}$ khi chưa áp dụng “Đồng nhất thức Woodbury” nhé.
-
Cứ mỗi phép cộng/trừ giữa hai ma trận có khích thước $a \times b$ và $a \times b$ có chi phí là $a \times b$
- Cứ mỗi phép nhân giữa hai ma trận có khích thước $a \times b$ và $b \times c$ có chi phí là $a \times b \times c$
- Nghịch đảo ma trận vuông $a \times a$ sẽ có chi phí là $a^{3}$
$\mathbf{(A+UCV)^{-1}}$ bao gồm 2 phép nhân, 1 phép cộng và 1 phép nghịch đảo. Tổng chi phí tính toán lúc này sẽ là:
\[\mathbf{n \times k \times k + n \times k \times n + n \times n + n \times n \times n = n^{3} + n^{2}k + nk^{2}}\]$\mathbf{A^{-1} - A^{-1}U(C^{-1}+VA^{-1}U)^{-1}VA^{-1}}$ bao gồm 6 phép nhân, 2 phép cộng/trừ và 2 phép nghịch đảo của $\mathbf{C^{-1}}$ “ta đã giả sử biết trước $\mathbf{A^{-1}}$”. Lúc này chi phí tính toán là:
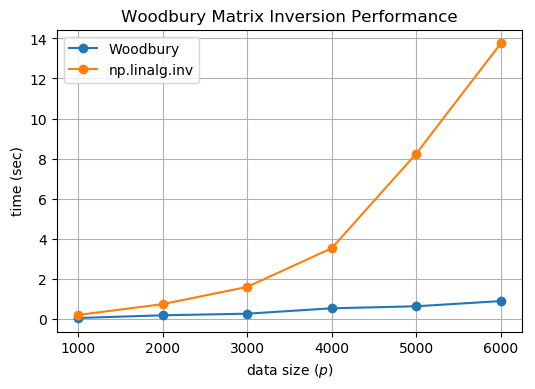
\[\mathbf{2k^{3} + 2k^{2}n + 4n^{2}k + k^{2} + n^{2}}\]Rõ ràng, bậc 3 của chúng ta lúc này đã đưa về cho $\mathbf{k}$ thay vì là $\mathbf{n}$ như lúc trước, và nếu $\mathbf{n \gg k}$ thì thật sự, tốc độ tính toán lúc này giảm đi rất nhiều lần. Hình bên dưới mô tả sự tăng trưởng của $\mathbf{n}$, ký hiệu trong hình sẽ là $\mathbf{p}$.
Note: hãy tính toán 6 phép nhân thông minh, đừng để bị dính vào phép nhân $\mathbf{n^{3}}$ nhé. Còn một điều nữa, “Đồng nhất thức ma trận Woodbury” còn có thể áp dụng cho trường hợp ma trận $\mathbf{A}$ là ma trận tam giác.
Vậy điều này có nghĩa gì 🤔🤔🤔, hãy chờ đợi bí mật được khai phá ở mục tiếp theo nhé.
Nào hãy cùng mình chứng minh về “Đồng nhất thức ma trận Woodbury” nhé.
Ta sẽ bắt đầu từ hai biểu thức cơ bản sau:
\[\mathbf{(I+P)^{-1} = (I+P^{-1})(I+P-P) = I - (I+P)^{-1}P} \hspace{1cm} (\text{2.2 *})\] \[\mathbf{P + PQP = P(I + QP) = (I + PQ)P}\] \[Suy\space ra:\space \mathbf{(I + PQ)^{-1}P = P(I + QP)^{-1}} \hspace{1cm} (\text{2.2 **})\]Từ đó ta khai triển biểu thức:
\[\begin{equation*} \begin{split} \mathbf{(A+UCV)^{-1}} & = \mathbf{(A[I+A^{-1}UCV])^{-1}} \\ & = \mathbf{\left[I +A^{-1}UCV\right]^{-1}A^{-1}} \\ & = \mathbf{\left[I - (I+A^{-1}UCV)^{-1}A^{-1}UCV\right]A^{-1}},\space \text{dùng biểu thức (\text{2.2 *})}\space P = A^{-1}UCV\\ & = \mathbf{A^{-1} - (I+A^{-1}UCV)^{-1}A^{-1}UCVA^{-1}} \\ & = \mathbf{A^{-1} - A^{-1}(I+UCVA^{-1})^{-1}UCVA^{-1}}, \space \text{dùng biểu thức (\text{2.2 **})}\space P = A^{-1}, Q = UCV\\ & = \mathbf{A^{-1} - A^{-1}U(I+CVA^{-1}U)^{-1}CVA^{-1}}, \space \text{dùng biểu thức (\text{2.2 **})}\space P = U, Q = CVA^{-1}, \space\\ & = \mathbf{A^{-1} - A^{-1}U(CC^{-1}+CVA^{-1}U)^{-1}CVA^{-1}}, \space \text{giả sử C khả nghịch}\\ & = \mathbf{A^{-1} - A^{-1}U(C^{-1} + VA^{-1}U)^{-1}C^{-1}CVA^{-1}}, \space \text{lấy C làm nhân tử chung}\\ & = \mathbf{A^{-1} - A^{-1}U(C^{-1}+VA^{-1}U)^{-1}VA^{-1}}, \space \text{điều phải chứng minh}\\ \end{split} \end{equation*}\]2.3 Conditional Gaussian distributions
Đây là một hướng giải thích cho hệ số Kalman. Các bạn hãy tập trung theo dõi nhé.
Chúng ta đã phân tích ở trên về $p(x^{t}|y^{t})$ , là hàm phân phối xác suất sẽ giúp ta cập nhật lại niềm tin về $x^{t}$ khi đã biết $y^{t}$.
Lúc này ta xét vector:
\[\mathbf{z} = \begin{bmatrix} \mathbf{x} \\ \mathbf{y} \end{bmatrix};\space \mathbf{x}\in \mathbb{R}^{p}, \space \mathbf{y}\in \mathbb{R}^{q}\]Và:
\[\mathbf{z} \thicksim \mathcal{N}(\mu_z,\Sigma_z) \Leftrightarrow \mathbf{z} \thicksim \mathcal{N}( \begin{bmatrix} \mu_x \\ \mu_y \end{bmatrix}, \begin{bmatrix} \Sigma_{xx} & \Sigma_{xy} \\ \Sigma_{yx} & \Sigma_{yy} \end{bmatrix})\]Dành cho những bạn chưa biết về ma trận covariance này có thể đọc thêm ở đây Multivariate Gaussian Distribution. Đặc tình của ma trận covariance này chính là:
\[\mathbf{\Sigma_z^\mathsf{T} = \Sigma_z \space\text{và}\space \Sigma_{xy}^\mathsf{T} = \Sigma_{yx}}\]Xét ma trận nghịch đảo của $\mathbf{\Sigma_z}$ và áp dụng Schur Complement of matrix đã trình bày ở mục 2.1:
\[\mathbf{\Sigma_z^{-1}} = \begin{bmatrix} \mathbf{\Sigma_{xx}} & \mathbf{\Sigma_{xy}} \\ \mathbf{\Sigma_{yx}} & \mathbf{\Sigma_{yy}} \end{bmatrix}^{-1} = \begin{bmatrix} \mathbf{ L^{-1}} & \mathbf{-L^{-1}\Sigma_{xy}\Sigma_{yy}^{-1}} \\ \mathbf{-\Sigma_{yy}^{-1}\Sigma_{yx}L^{-1}} & \mathbf{\Sigma_{yy}^{-1} + \Sigma_{yy}^{-1}\Sigma_{yx}L^{-1}\Sigma_{xy}\Sigma_{yy}^{-1}} \end{bmatrix} = \begin{bmatrix} \mathbf{\Lambda_{xx}} & \mathbf{\Lambda_{xy}} \\ \mathbf{\Lambda_{yx}} & \mathbf{\Lambda_{yy}} \end{bmatrix} \hspace{1cm} (\text{2.3-1})\] \[\text{Với: } \mathbf{L = \Sigma_{xx} - \Sigma_{xy}\Sigma_{yy}^{-1}\Sigma_{yx}}\]Với kích thước của từng $\mathbf{\Lambda_{xx},\space\Lambda_{xy},\space\Lambda_{yx},\space\Lambda_{yy}}$ sẽ tương ứng với $\mathbf{\Sigma_{xx},\space\Sigma_{xy},\space\Sigma_{yx},\space\Sigma_{yy}}$
Bây giờ chúng ta hãy viết lại khoảng cách Mahalanobis của hàm phân phối xác suất Gaussian nhé, có thể đọc ở đây nếu bạn chưa biết Multivariate Gaussian Distribution.
\[\begin{equation*} \begin{split} \mathbf{\left(z-\mu_z\right)^{\mathsf{T}}\Sigma_{z}^{-1}\left(z-\mu_z\right)} & = \quad \begin{bmatrix} \mathbf{x} - \mu_{x} \\ \mathbf{y} - \mu_{y} \end{bmatrix}^{\mathsf{T}} \begin{bmatrix} \mathbf{\Lambda_{xx}} & \mathbf{\Lambda_{xy}} \\ \mathbf{\Lambda_{yx}} & \mathbf{\Lambda_{yy}} \end{bmatrix} \begin{bmatrix} \mathbf{x} - \mu_{x} \\ \mathbf{y} - \mu_{y} \end{bmatrix} \\[6pt] & = \quad \mathbf{\left(x-\mu_x\right)^{\mathsf{T}}\Lambda_{xx}^{-1}\left(x-\mu_x\right)} + \mathbf{\left(x-\mu_x\right)^{\mathsf{T}}\Lambda_{xy}^{-1}\left(y-\mu_y\right)}\\[6pt] &\quad + \mathbf{\left(y-\mu_y\right)^{\mathsf{T}}\Lambda_{yx}^{-1}\left(x-\mu_x\right)} + \mathbf{\left(y-\mu_y\right)^{\mathsf{T}}\Lambda_{yy}^{-1}\left(y-\mu_y\right)} \hspace{1cm} (\text{2.3 I}) \\[6pt] & \text{Sử dụng (\text{2.3-1}) Schur Complement of matrix} \\[6pt] & = \quad (\mathbf{x} - \mathbf{\mu_x})^\mathsf{T} \mathbf{L} (\mathbf{x} - \mathbf{\mu_x}) - (\mathbf{x} - \mathbf{\mu_x})^\mathsf{T} \mathbf{L} \mathbf{\Sigma_{xy}} \mathbf{\Sigma}_{yy}^{-1} (\mathbf{y} - \mathbf{\mu_y}) \\[6pt] &\quad - (\mathbf{y} - \mathbf{\mu_y})^\mathsf{T} \mathbf{\Sigma}_{yy}^{-1} \mathbf{\Sigma}_{yx} \mathbf{L} (\mathbf{x} - \mathbf{\mu_x}) + (\mathbf{y} - \mathbf{\mu_y})^\mathsf{T} \mathbf{\Sigma}_{yy}^{-1} (\mathbf{y} - \mathbf{\mu_y}) \\[6pt] &\quad + (\mathbf{y} - \mathbf{\mu_y})^\mathsf{T} \mathbf{\Sigma}_{yy}^{-1} \mathbf{\Sigma}_{yx} \mathbf{L} \mathbf{\Sigma_{xy}} \mathbf{\Sigma}_{yy}^{-1} (\mathbf{y} - \mathbf{\mu_y}) \\[6pt] &= \quad (\mathbf{x} - (\mathbf{\mu_x} + \mathbf{\Sigma_{xy}} \mathbf{\Sigma}_{yy}^{-1} (\mathbf{y} - \mathbf{\mu_y})))^\mathsf{T} \mathbf{L} (\mathbf{x} - (\mathbf{\mu_x} + \mathbf{\Sigma_{xy}} \mathbf{\Sigma}_{yy}^{-1} (\mathbf{y} - \mathbf{\mu_y}))) \\[6pt] &\quad + (\mathbf{y} - \mathbf{\mu_y})^\mathsf{T} \mathbf{\Sigma}_{yy}^{-1} (\mathbf{y} - \mathbf{\mu_y}) \hspace{1cm} (\text{2.3 II}) \\[6pt] &= \quad (\mathbf{x} - \mathbf{\mu}_*)^\mathsf{T} \mathbf{L} (\mathbf{x} - \mathbf{\mu}_*) + (\mathbf{y} - \mathbf{\mu_y})^\mathsf{T} \mathbf{\Sigma}_{yy}^{-1} (\mathbf{y} - \mathbf{\mu_y}) \hspace{1cm} \text{(2.3-2)}\\[6pt] \end{split} \end{equation*}\]Với:
\[\mu_* = \mathbf{\mu_x} + \mathbf{\Sigma_{xy}} \mathbf{\Sigma}_{yy}^{-1} (\mathbf{y} - \mathbf{\mu_y}),\space\mathbf{L = \Sigma_{xx} - \Sigma_{xy}\Sigma_{yy}^{-1}\Sigma_{yx}} \hspace{1cm} \text{(2.3-3)}\]Ta có hàm phân phối xác suất của $\mathbf{z}$:
\[\large \mathbf{ p(z) = p(x,y) = \frac {\mathbf{e^{\frac {1} {2} \left(z-\mu_z\right)^{\mathsf{T}}\Sigma_{z}^{-1}\left(z-\mu_z\right)}}} {\mathbf{\sqrt{(2\pi)^{p+q} |\Sigma_z|}}} }\]Và hàm phân phối xác suất của $\mathbf{y}$:
\[\large \mathbf{ p(y) = \frac {\mathbf{e^{\frac {1} {2} \left(y-\mu_y\right)^{\mathsf{T}}\Sigma_{y}^{-1}\left(y-\mu_y\right)}}} {\mathbf{\sqrt{(2\pi)^{q}|\Sigma_y|}}} }\]Từ $\text{(1-3)}$ (đã bỏ yếu tố thời gian) ta có:
\[\large p(x|y) = \frac{p(y,x)}{p(y)} = \frac {\mathbf{\sqrt{(2\pi)^{q}|\Sigma_y|}\times e^{\frac {1} {2} \left(z-\mu_z\right)^{\mathsf{T}}\Sigma_{z}^{-1}\left(z-\mu_z\right)}}} {\mathbf{\sqrt{(2\pi)^{p+q}|\Sigma_z|}\times e^{\frac {1} {2} \left(y-\mu_y\right)^{\mathsf{T}}\Sigma_{y}^{-1}\left(y-\mu_y\right)}}}\]Sử dụng $\text{(2.3-2)}$:
\[\large p(x|y) = \frac {\mathbf{\sqrt{(2\pi)^{q}|\Sigma_y|}\times e^{\frac {1} {2} \left(z-\mu_z\right)^{\mathsf{T}}\Sigma_{z}^{-1}\left(z-\mu_z\right)}}} {\mathbf{\sqrt{(2\pi)^{p+q}|\Sigma_z|}\times e^{\frac {1} {2} \left(y-\mu_y\right)^{\mathsf{T}}\Sigma_{y}^{-1}\left(y-\mu_y\right)}}} = \frac {\mathbf{\sqrt{(2\pi)^{q}|\Sigma_y|}}} {\mathbf{\sqrt{(2\pi)^{p+q}|\Sigma_z|}}} \mathbf{e^{\frac {1} {2} (\mathbf{x} - \mathbf{\mu}_*)^\mathsf{T} \mathbf{L} (\mathbf{x} - \mathbf{\mu}_*)}}\]Lúc này $p(x|y)$ đã ra hình dáng của hàm phân phối xác suất Gaussian, hãy thử kiểm tra xem biểu thức dưới đây có bằng nhau hay không:
\[\large \frac {\mathbf{\sqrt{(2\pi)^{q} |\Sigma_y|}}} {\mathbf{\sqrt{(2\pi)^{p+q} |\Sigma_z|}}} = \frac {1} {\mathbf{\sqrt{(2\pi)^{p}|L|}}}\]Phân tích về trái của đẳng thức.
\[\large \begin{equation*} \begin{aligned} \frac {\mathbf{\sqrt{(2\pi)^{q}|\Sigma_y|}}} {\mathbf{\sqrt{(2\pi)^{p+q}|\Sigma_z|}}} & = \sqrt\frac {\mathbf{\left|\Sigma_y\right|\left|\Sigma_z\right|^{-1}}} {\mathbf{(2\pi)^{p}}} \\[6pt] & = \sqrt\frac {\mathbf{\left|\Sigma_{yy}\right| \left| \begin{matrix} \mathbf{\Sigma_{xx}} & \mathbf{\Sigma_{xy}} \\ \mathbf{\Sigma_{yx}} & \mathbf{\Sigma_{yy}} \end{matrix} \right|^{-1}}} {\mathbf{(2\pi)^{p}}} \\[6pt] & = \sqrt\frac { \mathbf{\left|\Sigma_{yy}\right| \left|\Sigma_{yy}\right|^{-1} \left|\Sigma_{xx} - \Sigma_{xy}\Sigma_{yy}^{-1}\Sigma_{yx}\right|^{-1}} } {\mathbf{(2\pi)^{p}}} \hspace{1cm} \text{(2.3-III)} \\[6pt] & = \sqrt\frac {1} {\mathbf{(2\pi)^{p}} \mathbf{ \left|\Sigma_{xx} - \Sigma_{xy}\Sigma_{yy}^{-1}\Sigma_{yx}\right|} }\\[6pt] & = \frac {1} {\mathbf{\sqrt{(2\pi)^{p}|L|}}} \hspace{1cm} \text{(điều phải chứng minh)} \end{aligned} \end{equation*}\]Vậy ta có thể kết luận rằng:
\[\large p(x|y) = \frac {p(x,y)} {q(y)} = \frac {1} {\mathbf{\sqrt{(2\pi)^{p}|L|}}} \mathbf{e^{\frac {1} {2} (\mathbf{x} - \mathbf{\mu}_*)^\mathsf{T} \mathbf{L} (\mathbf{x} - \mathbf{\mu}_*)}} \hspace{1cm} \text{(2.3-4)}\]Từ $\text{(2.3-3)}$:
\[\mu_* = \mathbf{\mu_x} + \mathbf{\Sigma_{xy}} \mathbf{\Sigma}_{yy}^{-1} (\mathbf{y} - \mathbf{\mu_y}),\space\mathbf{L = \Sigma_{xx} - \Sigma_{xy}\Sigma_{yy}^{-1}\Sigma_{yx}} \hspace{1cm} \text{(2.3-3)}\]Đến đây đã gần như là hoàn thiện, hãy đi sâu vào nữa để ra được kết quả nhé.
🤓🤓🤓 Hãy chú ý nhé, lần này sẽ thêm yếu tố thời gian vào đấy, kẻo bị loạn mắt.
Trong bài trước, nếu bạn đã đọc kỹ sẽ biết được.
\[\mathbf{ p(x|y) = p(x^{t+1}|y^{t+1}) }\]Vì thế ở đây ta sẽ chú thích một số ký hiệu đã dùng ở trên:
\[\begin{equation*} \begin{aligned} \mathbf{\mu_x} &= \mathbf{\mu_{x^{t+1}}} \hspace{1cm} (\text{2.3-5}) \\[6pt] \mathbf{\Sigma_{xx} = \Sigma_{x^{t+1}}} &= \mathbf{F\Sigma_{x^{t}}F^{\mathsf{T}}+Q} \hspace{1cm} (\text{2.3-6}) \\[6pt] \mathbf{\mu_y = H\mu_x} &= \mathbf{H\mu_x^{t+1}} \hspace{1cm} (\text{2.3-7}) \\[6pt] \mathbf{\Sigma_{yy} = \Sigma_{y^{t+1}} } &= \mathbf{ H\Sigma_{x^{t + 1}}H^{\mathsf{T}}+R} \hspace{1cm} (\text{2.3-8}) \\[6pt] \mathbf{\Sigma_{xy}} &= \mathbf{\Sigma_{x^{t+1}} H^{\mathsf{T}}} \hspace{1cm} (\text{2.3-9}) - (\text{2.3-IV}) \\[6pt] \mathbf{\Sigma_{yx}} = \mathbf{\Sigma_{xy}^{\mathsf{T}}} = \mathbf{H\Sigma_{x^{t+1}}^{\mathsf{T}}} &= \mathbf{H\Sigma_{x^{t+1}}} \hspace{1cm} (\text{2.3-10}) \end{aligned} \end{equation*}\]Thế $\text{(2.3-5)}$ $\text{(2.3-6)}$ $\text{(2.3-7)}$ $\text{(2.3-8)}$ $\text{(2.3-9)}$ $\text{(2.3-10)}$ vào $\text{(2.3-3)}$
\[\mu_* = \mu_{x|y} = \mu_{x^{t+1}|y^{t+1}} = \mathbf{\mu_{x^{t+1}}} + \mathbf{\Sigma_{x^{t+1}} H^{\mathsf{T}}} \mathbf{(H\Sigma_{x^{t+1}}H^{\mathsf{T}}+R)^{-1}} (\mathbf{y}^{t+1} - H\mu_{x^{t+1}})\] \[\begin{equation*} \begin{aligned} \mathbf{L} = \mathbf{\Sigma_{x|y}} = \mathbf{\Sigma_{x^{t+1}|y^{t+1}}} &= \mathbf{\Sigma_{xx} - \Sigma_{xy}\Sigma_{yy}^{-1}\Sigma_{yx}} \\[6pt] &= \mathbf{\Sigma_{x^{t+1}} - \Sigma_{x^{t+1}} H^{\mathsf{T}} (H\Sigma_{x^{t + 1}}H^{\mathsf{T}}+R)^{-1}H\Sigma_{x^{t+1}}}\\[6pt] \end{aligned} \end{equation*}\]Gọi $\mathbf{K}$ là hệ số Kalman:
\[\mathbf{K^{t+1} = \Sigma_{x^{t+1}}\mathbf{H}^{\mathbf{T}} (H\Sigma_{x^{t+1}}H^{\mathsf{T}} + R)^{-1}} \hspace{1cm} \text{2.3-11}\]Ta có:
\[\begin{equation*} \begin{aligned} \mu_{x^{t+1}|y^{t+1}} &= \mathbf{\mu_x^{t+1}} + \mathbf{K^{t+1}} (\mathbf{y}^{t+1} - H\mu_x^{t+1}) \hspace{1cm} \text{(2.3-12)}\\[6pt] \mathbf{\Sigma_{x^{t+1}|y^{t+1}}} &= \mathbf{\Sigma_{x^{t+1}} - K^{t+1}H\Sigma_{x^{t+1}}}\\[6pt] &= \mathbf{(I - K^{t+1}H)\Sigma_{x^{t+1}}}\\[6pt] &= \mathbf{\Sigma_{x^{t+1}}(I - K^{t+1}H)}\hspace{1cm} \text{(2.3-12)-(2.3-V)} \end{aligned} \end{equation*}\]Vậy là hệ số Kalman và bước cập nhật ở phần 1 đã được chứng minh tại đây, hãy cùng tiếp tục đến với hướng tiếp cận tiếp theo nhé.
3 Bayes’ theorem for Gaussian variables
Mỏi tay quá!!! Đợi mình thêm nhá.
4 Giải thích về chú thích cho các mục.
Note: Mình sẽ giải thích kết quả của Mahalanobis ở trên cho đọc giả dễ hiểu và dễ dàng tiếp cận hơn.
$(\text{2.3-I})$ Ở đây là một cách viết lại của phép nhân ma trận, mình sẽ ví dụ một cách dễ hiểu để bạn hiểu được:
\[\begin{bmatrix} \mathbf{x} - \mu_{x} \\ \mathbf{y} - \mu_{y} \end{bmatrix}^{\mathsf{T}} = \begin{bmatrix} \mathbf{x} - \mu_{x} \\ 0 \end{bmatrix}^{\mathsf{T}} + \begin{bmatrix} 0 \\ \mathbf{y} - \mu_{y} \end{bmatrix}^{\mathsf{T}}\]Lúc này kết quả của Mahalanobis distance lúc này chính là:
\[\begin{bmatrix} \mathbf{x} - \mu_{x} \\ \mathbf{y} - \mu_{y} \end{bmatrix}^{\mathsf{T}} \begin{bmatrix} \mathbf{\Lambda_{xx}} & \mathbf{\Lambda_{xy}} \\ \mathbf{\Lambda_{yx}} & \mathbf{\Lambda_{yy}} \end{bmatrix} \begin{bmatrix} \mathbf{x} - \mu_{x} \\ \mathbf{y} - \mu_{y} \end{bmatrix} = \begin{bmatrix} \mathbf{x} - \mu_{x} \\ 0 \end{bmatrix}^{\mathsf{T}} \begin{bmatrix} \mathbf{\Lambda_{xx}} & \mathbf{\Lambda_{xy}} \\ \mathbf{\Lambda_{yx}} & \mathbf{\Lambda_{yy}} \end{bmatrix} \begin{bmatrix} \mathbf{x} - \mu_{x} \\ \mathbf{y} - \mu_{y} \end{bmatrix} + \begin{bmatrix} 0 \\ \mathbf{y} - \mu_{y} \end{bmatrix}^{\mathsf{T}} \begin{bmatrix} \mathbf{\Lambda_{xx}} & \mathbf{\Lambda_{xy}} \\ \mathbf{\Lambda_{yx}} & \mathbf{\Lambda_{yy}} \end{bmatrix} \begin{bmatrix} \mathbf{x} - \mu_{x} \\ \mathbf{y} - \mu_{y} \end{bmatrix}\]Tương tự, hãy chia các ma trận thành tổng các ma trận có các thành phần khuyết bằng 0, kết quả của Mahalanobis distance là một số, vì thế ta có thể lược bỏ phần khuyết bằng 0 nếu nó không ảnh hưởng đến kết quả.
$(\text{2.3-II})$ Nếu ở bước này có ai quá nhanh và không hiểu thì mình xin được trình bày chậm lại như sau (Các ma trận có cùng kích thước, vì thế chúng ta có thể gom nhóm lại với nhau để làm nhân tử chung).
\[\begin{equation*} \begin{aligned} &\quad (\mathbf{x} - \mathbf{\mu_x})^\mathsf{T} \mathbf{L} (\mathbf{x} - \mathbf{\mu_x}) - (\mathbf{x} - \mathbf{\mu_x})^\mathsf{T} \mathbf{L} \mathbf{\Sigma_{xy}} \mathbf{\Sigma}_{yy}^{-1} (\mathbf{y} - \mathbf{\mu_y}) \\[6pt] &\quad - (\mathbf{y} - \mathbf{\mu_y})^\mathsf{T} \mathbf{\Sigma}_{yy}^{-1} \mathbf{\Sigma}_{yx} \mathbf{L} (\mathbf{x} - \mathbf{\mu_x}) + (\mathbf{y} - \mathbf{\mu_y})^\mathsf{T} \mathbf{\Sigma}_{yy}^{-1} \mathbf{\Sigma}_{yx} \mathbf{L} \mathbf{\Sigma_{xy}} \mathbf{\Sigma}_{yy}^{-1} (\mathbf{y} - \mathbf{\mu_y}) \\[6pt] = &\quad \mathbf{(x-\mu_x)^{\mathsf{T}}L\left[(x-\mu_x) - \Sigma_{xy}\Sigma_{yy}^{-1}(y-\mu_y)\right]} \\[6pt] &\quad - \mathbf{(y-\mu_y)^{\mathsf{T}}\Sigma_{yy}^{-1}\Sigma_{yx}L\left[(x-\mu_x) - \Sigma_{xy}\Sigma_{yy}^{-1}(y-\mu_y)\right]}\\[6pt] = &\quad \mathbf{\left[(x-\mu_x)^{\mathsf{T}} - (y-\mu_y)^{\mathsf{T}}\Sigma_{yy}^{-1}\Sigma_{yx}\right]L\left[(x-\mu_x) - \Sigma_{xy}\Sigma_{yy}^{-1}(y-\mu_y)\right]} \hspace{1cm} (\mathbf{A^{\mathsf{T}} + B^{\mathsf{T}} = (A+B)^{\mathsf{T}}}) \\[6pt] = &\quad \mathbf{\left[(x-\mu_x) - \Sigma_{xy}\Sigma_{yy}^{-1}(y-\mu_y)\right]^{\mathsf{T}}L\left[(x-\mu_x) - \Sigma_{xy}\Sigma_{yy}^{-1}(y-\mu_y)\right]} \end{aligned} \end{equation*}\]$\text{2.3-III}$ Sử dụng Schur complements và Block-matrix
\[\begin{equation*} \begin{aligned} \left|\begin{matrix} \mathbf{A}&\mathbf{B}\\ \mathbf{B^{\mathsf{T}}}&\mathbf{D} \end{matrix}\right| &= \left|\begin{matrix} \mathbf{I}&\mathbf{BD^{-1}}\\ \mathbf{0}&\mathbf{I} \end{matrix}\right| \left|\begin{matrix} \mathbf{A-BD^{-1}C}&\mathbf{0}\\ \mathbf{0}&\mathbf{D} \end{matrix}\right| \left|\begin{matrix} \mathbf{I}&\mathbf{0}\\ \mathbf{D^{-1}C}&\mathbf{I} \end{matrix}\right| \\[6pt] &=\mathbf{1\times|D|\times\left|A-BD^{-1}C\right|\times 1} \end{aligned} \end{equation*}\]$\text{2.3-IV}$
\[\begin{equation*} \begin{aligned} \mathbf{\Sigma_{xy}} &= \mathbf{\mathbb{E}\left[(x-\mu_x) (y-\mu_y)^{\mathsf{T}}\right]} \hspace{1cm} (\text{Định nghĩa ma trận covariance}) \\[6pt] &= \mathbf{\mathbb{E}\left[\Delta x \Delta y^{\mathsf{T}}\right]} \hspace{1cm} (\Delta x = (x-\mu_x),\space \Delta y = (y-\mu_y))\\[6pt] &= \mathbf{\mathbb{E}\left[\Delta x (\mathbf{H}*\Delta x+ \Delta\mathbf{v})^{\mathsf{T}}\right]} \\[6pt] &= \mathbf{\mathbb{E}\left[\Delta x \Delta x ^{\mathsf{T}} \mathbf{H}^{\mathsf{T}}+ \Delta x\Delta v^{\mathsf{T}}\right]} \\[6pt] &= \mathbf{\mathbb{E}\left[\Delta x \Delta x ^{\mathsf{T}} \right]H^{\mathsf{T}}+ \mathbb{E}\left[\Delta x\Delta v^{\mathsf{T}}\right]} \\[6pt] &= \mathbf{\Sigma_x H^{\mathsf{T}}} \hspace{1cm} (\text{giả sử x và v độc lập} \Leftrightarrow \Sigma_{xv} = 0) \\[6pt] &= \mathbf{\Sigma_{x^{t+1}} H^{\mathsf{T}}} \end{aligned} \end{equation*}\]$\text{2.3-IV}$
\[\begin{equation*} \begin{aligned} \mathbf{\Sigma_{x^{t+1}|y^{t+1}}} &= \mathbf{(I - K^{t+1}H)\Sigma_{x^{t+1}}} \hspace{1cm} \mathbf{\Sigma_{x^{t+1}|y^{t+1}},\space \Sigma_{x^{t+1}}}\space\text{đối xứng}\\[6pt] \mathbf{\Sigma_{x^{t+1}|y^{t+1}}\Sigma_{x^{t+1}}^{-1}} &= \mathbf{(I - K^{t+1}H)} \hspace{1cm} \Rightarrow \mathbf{(I - K^{t+1}H)} \space\text{đối xứng}\\[6pt] \mathbf{\Sigma_{x^{t+1}|y^{t+1}}} &= \mathbf{\left[(I - K^{t+1}H)\Sigma_{x^{t+1}}\right]}^{\mathsf{T}}\\[6pt] &= \mathbf{\Sigma_{x^{t+1}}(I - K^{t+1}H)} \end{aligned} \end{equation*}\]